Introduction

Autonomous drone racing is a test of both speed and brains. At the start line, dozens of drones hover in place, motors humming and sensors locked on their first turn. Victory depends on more than raw power - each drone must sense the track, plan a path, and adjust its motors every few milliseconds without missing a beat.

Traditional methods struggle in this setting. Model-based controllers can follow a planned trajectory and recover from small disturbances, but they cannot learn from new situations on the fly. Pure reinforcement-learning agents learn quickly, yet they often ignore safety limits and break down when conditions change. Drones need a controller that combines learning ability with the discipline to stay within physical bounds.

Actor-Critic Model Predictive Control (AC-MPC) brings the best of both worlds. It combines model-free reinforcement learning with model-based predictive control, producing a policy that learns aggressive manoeuvres while still respecting hard constraints.

In this blog article, we explain the key pieces: Actor-Critic reinforcement learning, Model Predictive Control, and Differentiable MPC and show how their combination lets autonomous drones think, fly, and win both in simulation and on the real course.

The Problem with Traditional Methods

Limitations of Traditional Model Predictive Control (MPC) in Drone Racing

While MPC is widely praised for its precise control and real-time optimization capabilities, it struggles as drone racing tasks become more complex and demanding.

Here’s why:

• Heavy Manual Engineering: Every new task (like a different race track or gate layout) requires human experts to carefully design the cost function, manually tune hyperparameters (like weights for speed vs stability), and define a planning strategy. This makes development slow and labor-intensive.

• Overly Conservative Behavior: Because MPC relies on hand-crafted rules and worst-case assumptions, it often plays it safe(Slows down unnecessarily). This can lead to sub-optimal performance, especially when drones are expected to fly aggressively or operate near the edge of physical limits, something that's routine in drone racing.

• No Learning or Adaptation: MPC doesn’t improve over time. It has no memory of past mistakes or successes. In contrast, RL-based methods can learn to improve through trial and error, whereas MPC cannot.

• Fails at Discrete Mode-Switching: Some racing situations require drones to switch behaviors rapidly, for example, shifting from tight turns to steep dives. MPC, being continuous and smooth, struggles to adapt to these discrete changes in control strategy.

• Modular Structure Can Break Down: MPC systems are often built as modules (planner, tracker, estimator, controller). Errors in one module can propagate through the others, causing a cascading failure, e.g., a small planning error leads to poor control, which leads to a crash.

• Error Accumulation Over Time: If the system model isn’t perfect (and it's never perfect), MPC can accumulate small errors over each step. Over time, these inaccuracies build up, causing the drone to drift off its intended path or behave unpredictably.

Limitations of Traditional Reinforcement Learning in Drone Racing

While reinforcement learning (RL) has shown impressive results in learning complex behaviors from scratch, it also comes with major challenges, especially when applied to high-speed, real-world systems like racing drones.

Here’s why:

• Learning Everything From Scratch: Most model-free RL methods don’t use any prior knowledge about physics or drone dynamics. The system starts with zero understanding and must figure everything out just by trial and error. This makes training extremely slow, often requiring millions of simulation steps to learn even basic control.

• Lack of Generalization: RL policies often overfit to the environment they were trained in. If you change the wind speed, track layout, or drone weight even slightly, the policy can break down. This makes it unreliable in the real world, where conditions always change.

• Poor Robustness to Out-of-Distribution (OOD) States: If the drone ends up in a situation it didn’t see during training (like starting in the wrong position or being hit by a gust of wind), it often panics or fails. RL agents typically don’t know how to recover from unfamiliar scenarios.

• No Real-Time Adaptation: In racing, the drone must adapt quickly to disturbances. Pure RL policies don’t re-plan, they just react based on what they learned before.

Building Blocks

Actor Critic

In reinforcement learning, there’s often a trade-off between exploration and decision-making. Some methods focus purely on learning a value function (like Q-learning), while others directly learn a policy (like policy gradient methods).

Actor-Critic methods do both, and that’s their power.

Think of it like a two-part brain:

• The Actor is the decision-maker. It learns a policy (a mapping from states to actions) and decides what to do.

• The Critic is the evaluator. It learns a value function, estimating how good the current situation is (or how good the chosen action will be).

Popular algorithms like PPO, A3C, and DDPG are all based on Actor-Critic architectures.

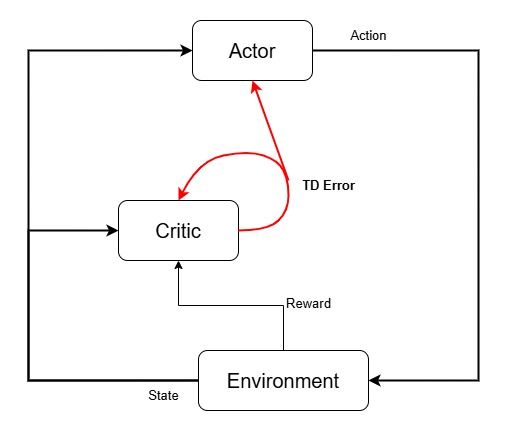
The Actor does not receive rewards directly. Instead, it relies on the Critic, which estimates the Temporal Difference (TD) error based on the received rewards and value predictions. This TD error is then used to update both the Actor and Critic networks.

The following equations represent the gradient update rules for the Actor and Critic:

Actor Network gradient update equation:

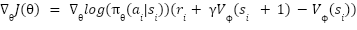
Critic Network Gradient update equation:

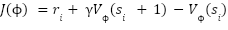
Model Predictive Control (MPC)

Model Predictive Control (MPC) has emerged as one of the most powerful control strategies in modern robotics and autonomous vehicle systems. With its inherent ability to handle constraints, anticipate future events, and optimize performance over a time horizon, MPC bridges the gap between classical control methods and modern autonomous system requirements.

This article is a deep technical dive into the formulation, operation, and application of MPC in the context of autonomous driving. It integrates concepts from the foundational literature, hands-on examples, and proven deployment strategies.

Overview of Model Predictive Control

Model Predictive Control is an advanced control technique that solves an online optimization problem at every time step. Given a model of the system dynamics, MPC predicts the future behavior of the system over a finite prediction horizon, optimizing a cost function while respecting system constraints.

Core Components (Explained):

• System Model: The mathematical model defines how the system evolves in response to control inputs. It can be either linear (e.g., state-space or transfer function models) or nonlinear (e.g., bicycle model for vehicles). A precise system model is critical because MPC relies on accurate future predictions based on this model. For example, in vehicle dynamics, a kinematic bicycle model or a dynamic model may be used depending on the desired fidelity.

• Prediction Horizon (N): This is the look-ahead window over which predictions and optimizations are made. The controller computes how the system will behave for the next N steps. A longer horizon provides better foresight but increases computational load. It balances between responsiveness and stability, often ranging between 10 to 50 steps for autonomous vehicle applications.

• Cost Function (Objective): The cost function is a mathematical expression that quantifies the performance of control actions over the prediction horizon. It typically consists of quadratic penalties on state errors (difference between predicted states and reference trajectory) and control effort. The standard form is: where Q penalizes deviation from the target state and R penalizes excessive actuator usage, ensuring smooth control.

• Constraints: MPC can handle a variety of constraints directly in the optimization process. These include:

96. Input constraints: Bounds on actuators such as throttle, brake, and steering angle.
97. State constraints: Restrictions on variables like speed, position, yaw angle, etc.
98. Output constraints: Often imposed indirectly via state constraints (e.g., lateral deviation from lane center).

Constraints ensure that the control strategy is safe, physically feasible, and legally compliant (e.g., staying within lane boundaries).

MPC in Practice

At the heart of MPC lies the idea of predicting the future behavior of a system and choosing control actions that minimize a predefined cost over a time horizon. Let’s break it down with a concrete example.

Scenario: Lane Keeping in Autonomous Driving

In the scenario of lane-keeping for autonomous driving, Model Predictive Control (MPC) is employed to keep the vehicle accurately centered within its lane over the next 5 seconds. The system begins with comprehensive knowledge of the vehicle’s current state, including its position, heading direction, and speed. It also leverages a precise model that describes how steering angles and acceleration commands influence future vehicle positioning.

Step 01 The first step, predicting the future trajectory, involves simulating how the vehicle will behave over a short prediction horizon, typically about 5 seconds into the future. This simulation occurs at regular intervals, such as every 0.1 seconds, resulting in around 50 prediction steps. For each sequence of potential control inputs (e.g., steering angle and acceleration combinations), MPC calculates the vehicle’s probable path forward in time, based on the current vehicle state and dynamic model.

Step 02 The second step, evaluating cost, assigns a numerical penalty to each potential trajectory. This cost rises whenever the vehicle drifts away from the lane center, indicating a loss in precision. It also increases if the vehicle exhibits excessive steering angles or experiences abrupt changes in acceleration or deceleration, which can reduce comfort and stability.

Step 03 Next, MPC enforces constraints to ensure the safety and feasibility of driving maneuvers. During this step, control sequences that violate constraints, such as exceeding the maximum or minimum allowed steering angles, surpassing speed limits, or straying out of the drivable area, are discarded. This filtering process ensures that all remaining control sequences represent practical and safe driving options.

Step 04 Once constraints have been applied, MPC proceeds to optimize by selecting the best control sequence, the one yielding the lowest cost while still satisfying all safety and feasibility constraints. This optimal sequence represents the most balanced trade-off between accuracy in lane-keeping, driving comfort, and safety.

Step 05 Finally, MPC applies only the first action from this optimal sequence to the vehicle, for example, a slight steering adjustment. Immediately afterward, the MPC process restarts with updated sensor data reflecting the vehicle’s new position and state. This continuous recalculation and updating process, known as the receding horizon principle, allows the autonomous vehicle to constantly refine its path and maintain precise lane alignment in real time.

Why This Works By continuously optimizing over a moving time window and accounting for how current decisions influence the future, MPC achieves a balance between immediate correction and long-term stability. It avoids the short-sightedness of reactive control and handles multi-variable, constrained scenarios naturally.

Application to Autonomous Vehicles

In autonomous driving, the vehicle must follow a trajectory while respecting road boundaries, avoiding obstacles, and obeying dynamic constraints. MPC fits perfectly due to:

• Trajectory tracking: Minimize deviation from a reference path.
• Dynamic feasibility: Adherence to vehicle dynamics (e.g., kinematic/dynamic bicycle model).
• Constraint handling: Ensure safety and comfort constraints (e.g., acceleration limits, steering angle bounds).

Implementation Workflow

134. Model Selection: Choose an appropriate vehicle model (kinematic or dynamic).
135. Linearization (if necessary): Nonlinear models are linearized around the current operating point.
136. State Estimation: Use sensor fusion (e.g., Kalman Filter) to obtain accurate state estimates.
137. Trajectory Generation: Provide a reference path (e.g., from global planner).
138. Solve Optimization: Use a Quadratic Programming (QP) solver or Sequential Quadratic Programming (SQP) in nonlinear cases.
139. Apply Control Input: Apply the first control input and repeat the cycle.

Example: CasADi + IPOPT for Nonlinear MPC CasADi is often used with IPOPT or OSQP solvers for fast nonlinear MPC implementations in Python/C++ environments.

Comparison to Other Controllers

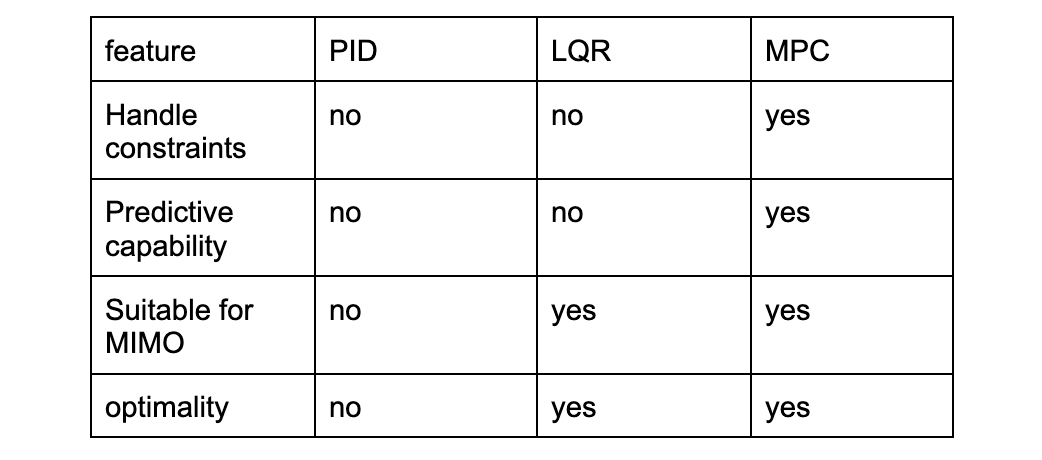
MPC is superior in constrained environments, especially where future prediction is critical. However, it comes at a computational cost, making real-time implementation challenging without proper optimizations or hardware acceleration.

Challenges and Considerations

• Real-time feasibility: Solving QP/NLP in milliseconds requires efficient solvers or warm-start strategies.
• Model fidelity: The accuracy of prediction depends on the accuracy of the model.
• Tuning Q, R, and horizon: Poor tuning can lead to oscillations, instability, or sluggish behavior.
• Obstacle avoidance integration: Coupling with perception modules requires real-time constraint adaptation.

Conclusion

Autonomous drone racing stretches both hardware and algorithms. Traditional control splits into two camps: model-based methods like MPC, which play safe but respond slowly, and model-free learning, which adapts fast but can ignore safety limits. Actor-Critic MPC bridges these worlds by pairing a neural policy that learns aggressive maneuvers with a predictive model that keeps every move within physics and safety boundaries. The result is a drone that slices through gates at speed without losing control.

This blend is useful far beyond racing. Any machine that must move quickly yet stay within tight constraints—self-driving cars, factory-floor robotic arms, even legged robots on rough terrain—can gain from the same recipe of planning, prediction, and continual learning. As processors get faster and solvers lighter, AC-MPC will move from lab demos to everyday machines, proving that autonomy can be both nimble and safe.

Stay tuned for Part 2, where we dive into Differentiable MPC and show how it teams up with Actor-Critic learning to build even faster, end-to-end trainable controllers.